Robust Calibration of Large Vision-Language Adapters

Balamurali Murugesan · Julio Silva-Rodríguez · Ismail Ben Ayed · Jose Dolz

ÉTS Montreal

ECCV 2024

Paper Code

Highlights

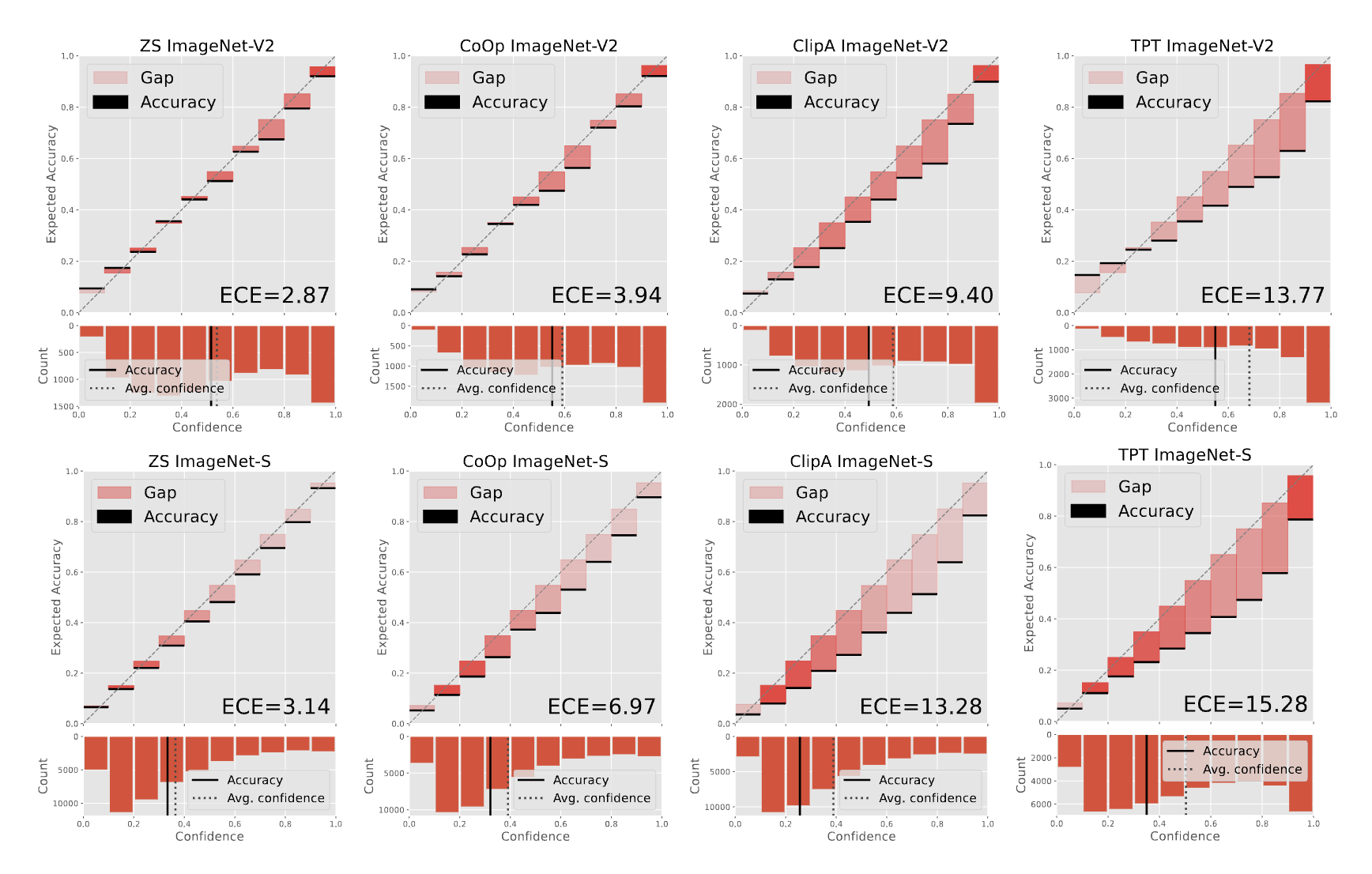
  • CLIP adaptation strategies, such as Adapters, Prompt Learning, and Test-Time Prompt Tuning, substantially degrade the calibration capabilities of the zero-shot baseline in the presence of distributional drift.
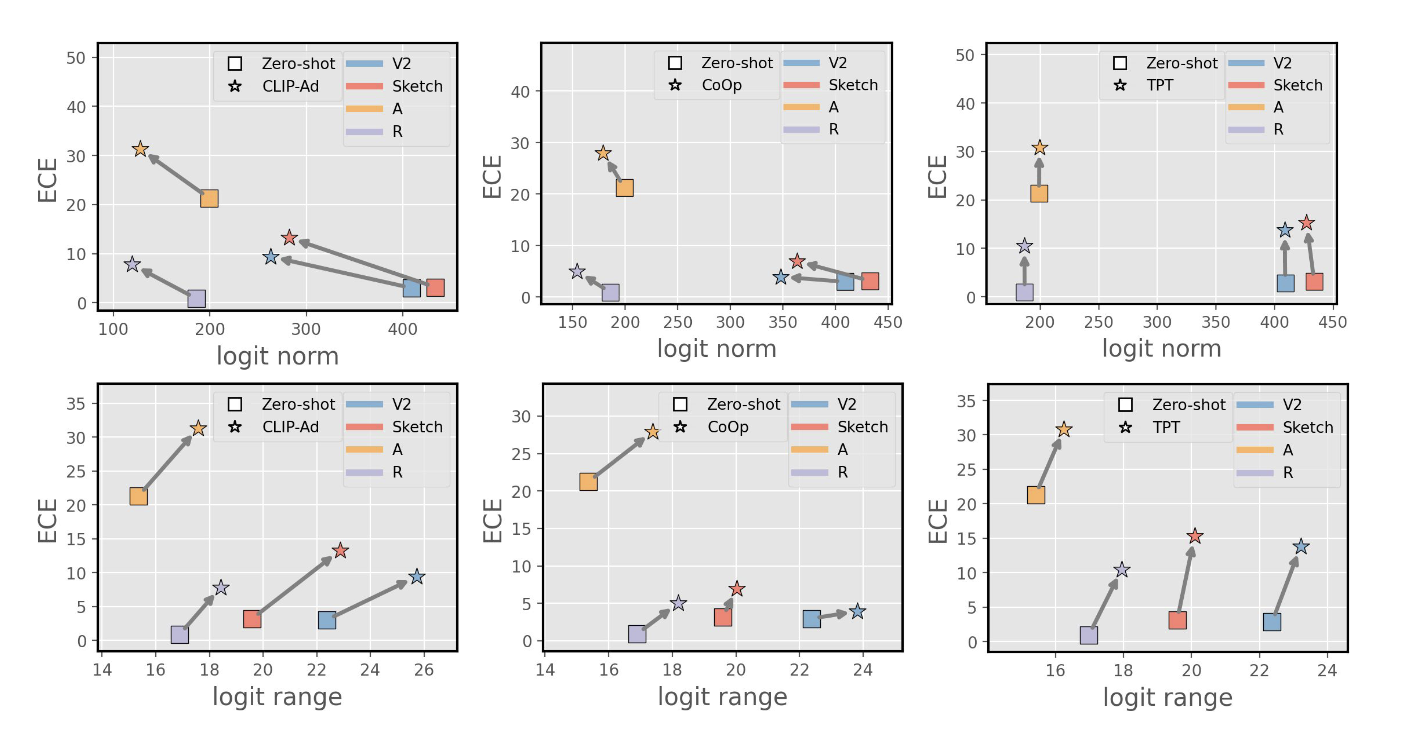
  • The underlying cause of miscalibration is, in fact, the increase of the logit ranges and not its norm.
  • A simple, and model-agnostic solutions, which consists in scaling the logit range of each sample based on the zero-shot logits either at training or inference time.
  • Comprehensive experiments on popular OOD classification benchmarks empirically demonstrate the effectiveness of our approaches to reduce the miscalibration error, while keeping the discriminative performance.

Motivation

Miscalibration on Out-of-distribution (OOD) samples.

Nature

Logit norm or logit range as the source of miscalibration?

Nature

Solution

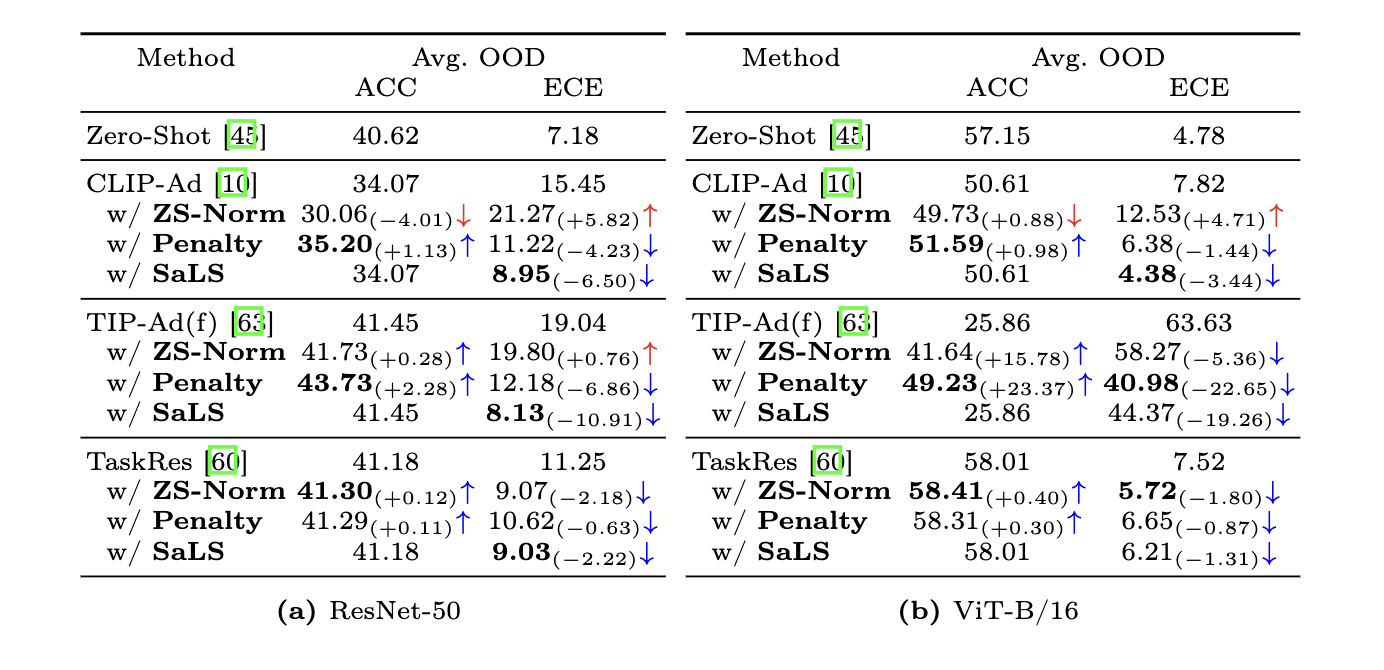
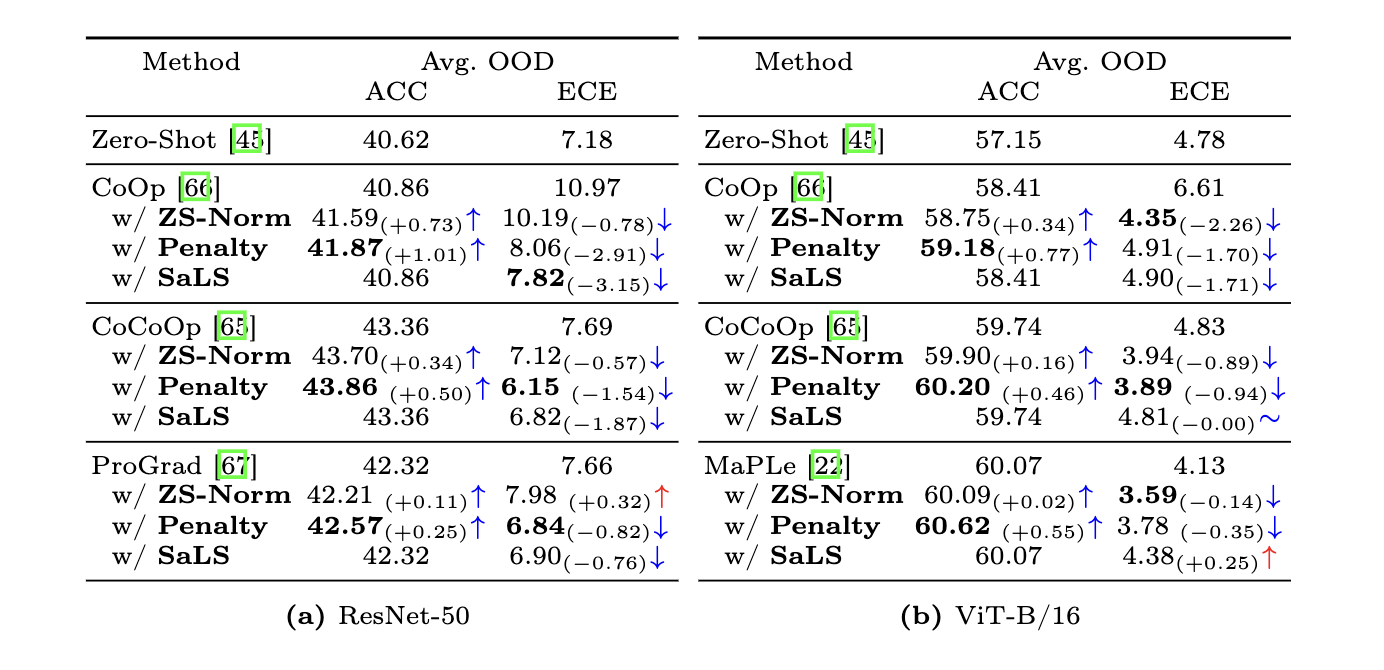
Formulation
$$ \text{minimize} \qquad \mathbf{H}(\mathbf{Y},\mathbf{P}) $$ $$ \text{subject to} \qquad l^{\text{ZS-min}}_{i} \mathbf{1} \leq l_i \leq l^{\text{ZS-max}}_{i} \mathbf{1} \qquad \forall i \in D$$ Solution 1 : Sample-adaptive logit scaling (SaLS) $$ l'_i=\frac{(l^{\text{ZS-max}}_{i}-l^{\text{ZS-min}}_{i})}{(l^{\text{max}}_{i}-l^{\text{min}}_{i})} (l_i-l^{\text{min}}_{i} \mathbf{1})+l^{\text{ZS-min}}_{i} \mathbf{1}$$ Solution 2 : Zero-shot logit normalization (ZS-Norm) $$ \min_{\boldsymbol{\theta}} \; -\sum_{i\in S}\sum_{k=1}^K y_{ik}\log \frac{\exp{(l'_{ik})}}{\sum_{j=1}^{K}\exp{(l'_{ij})}}$$ Solution 3 : Explicit Penalty in the learning objective (Penalty) $$ \min_{\boldsymbol{\theta}} \; \mathbf{H}(\mathbf{Y},\mathbf{P}) + \lambda \sum_{i \in S} \sum_{k=1}^K (\text{ReLU}(l_{ik}-l^{\text{ZS-max}}_{i})+\text{ReLU}(l^{\text{ZS-min}}_{i}-l_{ik}))$$


Results

Adapters calibration

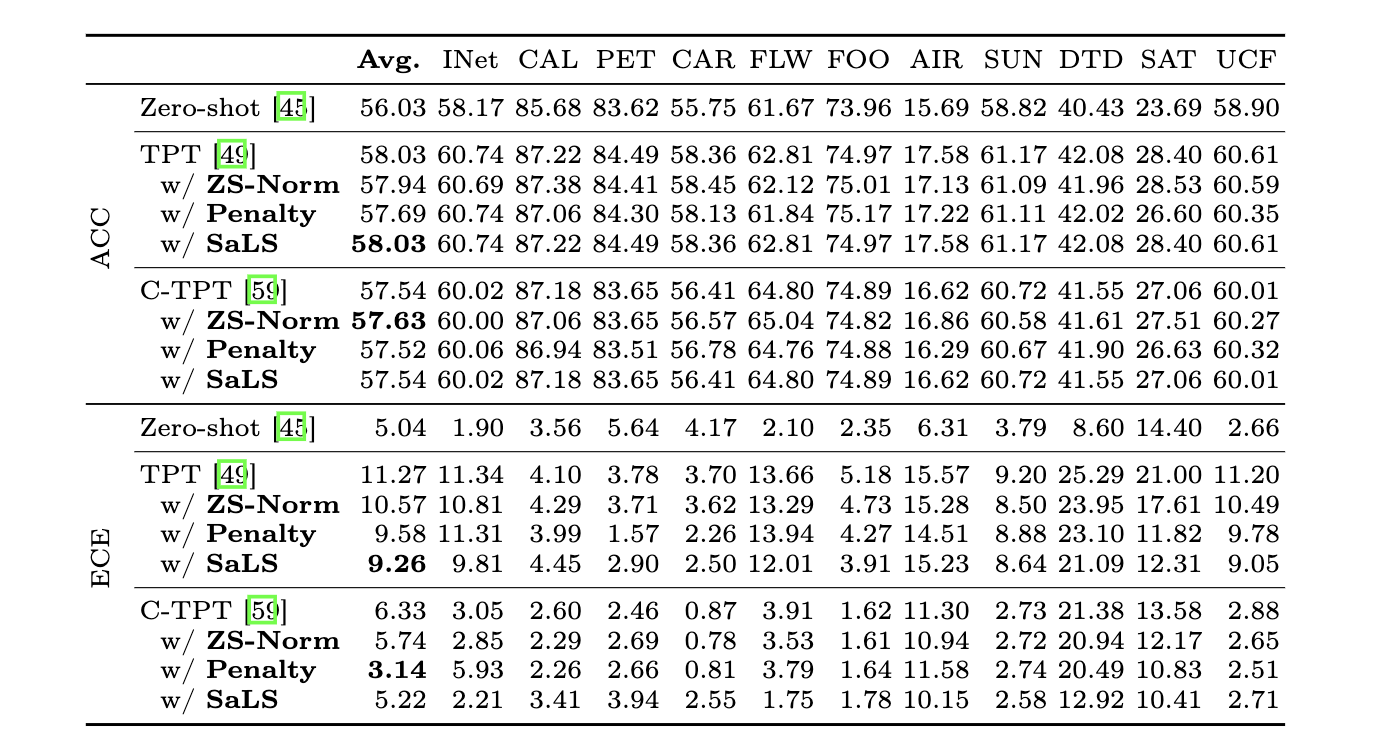
Nature

Prompt Learning calibration

Nature

Test-time Prompt Learning calibration

Nature

Citation

Please cite our paper if it is helpful to your work:

 @article{
        murugesan2024robust,
        title={Robust Calibration of Large Vision-Language Adapters},
        author={Murugesan, Balamurali and Silva-Rodriguez, Julio and Ayed, Ismail Ben and Dolz, Jose},
        journal={arXiv preprint arXiv:2407.13588},
        year={2024}
    }

Contact

Please feel free to contact us: balamurali.murugesan.1@ens.etsmtl.ca.